Skip to main content

· 8 min read

图结构和2种搜索算法入门​

​ 在数据的逻辑结构D=（KR）中，如果K中结点对于关系R的前趋和后继的个数不加限制，即仅含一种任意的关系，则称这种数据结构为图形结构

这是百度百科的解释，说人话， 图是一种数据结构，其中结点可以具有零个和多个相邻元素。 两个结点称为边。 结点也可以叫做顶点。

image-20220303200106136

1. 图的概念​

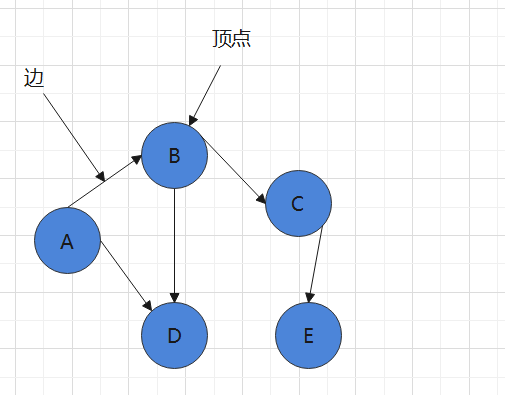
1) 顶点(vertex)

2) 边（edge)

3) 路径

A路径有: A -> B -> D,A -> B -> C -> E, B有路径 B -> D，B -> C -> E

4) 有向图和无向图(有向图指的是两个元素指两个元素有方向，无向图两个元素没有方向) 比如 A->B A->D

5) 带权图。 指的是这个边的值， 比如 A-> B 的边表示10公里， B -> C的边表示 5公里。

image-20220303200657735

2. 图的表示方式​

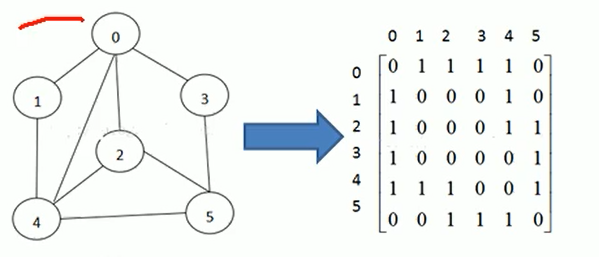
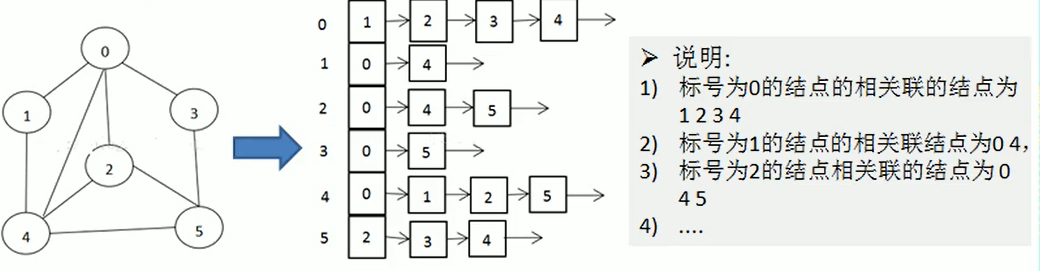
2.1 邻接矩阵​

邻接矩阵是表示图形中顶点的之间的关系的矩阵，对于n个 顶点的图而言， 矩阵的row和col 表示的是 1...n个点。如下图所示

2.2 邻接表​

  1. 邻接矩阵需要为第个顶点都分配n个边的空间， 其实有很多的边不存在，造成空间浪费

  2. 邻接表只关心边， 不关心不存在的边。 所以没有空间浪费， 邻接表由数组 + 链表组成

    image-20220303201115950

3. 图索算法​

图搜索算法有深度优先(dfs)，和广度优先(bfs)两种。

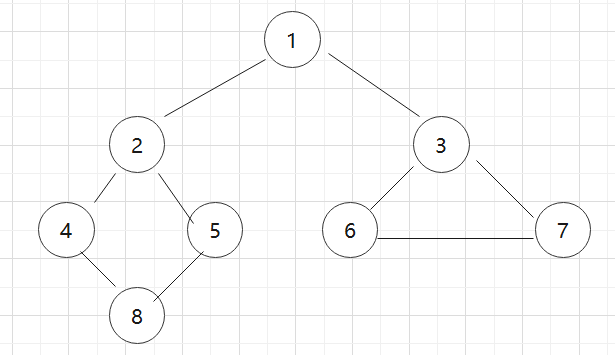
image-20220303201411405

如果从1 这个节点为起始点来遍历， 深度优先，和广度的顺序不相同。

深度优先搜索: 1 ，2，4，8，5，3，6，7

广度优先搜索： 1，2，3，4，5，6，7，8

由上面的遍历顺序我们可以发现深度是纵向遍历，而广度是横向遍历。

下面我们将编写两种算法和分析2种算法的具体执行流程。

3.1 使用代码实现邻接矩阵和邻接表​

3.1.1 邻接表的实现​

这里暂时先留下， 后面填坑

3.1.2 邻接矩阵​

下图是一个 邻接矩阵， 通过下面数据可以看到有以下关系

A - B , B - C, C-D 有连接关系， 下面的图也可以用数据结构2维数组来表示, 我们这里规定两个节点相交的时候值为1

int[][] = new int[4][4];
那么A - B ,在数组中表示为int[0][1] = 1,int[1][0] = 1.
那么B - C ,在数组中表示为int[0][1] = 1,int[1][0] = 1.
那么C - D ,在数组中表示为int[0][1] = 1,int[1][0] = 1.

image-20220304125146917

代码如下

    public static class Graph {
        // 顶点数据(vertex)
        private List<String> vertexts;
        // 边(节点相交数据)
        private int[][] edges;
        // 边的数量
        private int numberOfEdges;

        public Graph(int count) {
            vertexts = new ArrayList<>(count);
            edges = new int[count][count];
            isVeisited = new boolean[count];
        }

        /**
         * 插入顶点的数据
         * @param vertex
         */
        public void addVertex(String vertex) {
            vertexts.add(vertex);
        }

        public String getVertext(int index) {
            return vertexts.get(index);
        }
        /**
         * 
         * @param v1 第一个节点的索引
         * @param v2 第干个节点的索引
         * @param weight 权重（这里我们规定加入两个相交权重为1）
         */
        public void insertEdge(int v1, int v2, int weight) {
            edges[v1][v2] = weight;
            edges[v2][v1] = weight;
            numberOfEdges++;
        }
        public void insertEdge(int v1, int v2, int weight) {
            edges[v1][v2] = weight;
            edges[v2][v1] = weight;
            numberOfEdges++;
        }
        public void showGrpah() {
            for (int[] edge : edges) {
                System.out.println(Arrays.toString(edge));
            }
        }
        public String getValueByIndex(int index) {
            return vertexts.get(index);
        }
}

下面来测试一下代码, 假设有4个顶点分别是 数据分别为1，2，3，4，5，6，7，8 他们的索引分别是 0, 1,2,3 ,4，5，6，7，8 

public class GraphDemo {
    public static void main(String[] args) throws InterruptedException {
        // 插入8个顶点
        String[] Vertexs = {"1", "2", "3", "4", "5", "6", "7", "8"};
        Graph graph = new Graph(Vertexs.length);
        for (String s : Vertexs) {
            graph.addVertex(s);
        }

        // 插入8条边， 
        graph.insertEdge(0, 1, 1); // 这里的第一个参数0表示顶点1的索引，第二个参数表示数据为2的顶点的索引，第三个参数表示两个顶点相交。
        graph.insertEdge(0, 2, 1);
        graph.insertEdge(1, 3, 1);
        graph.insertEdge(1, 4, 1);
        graph.insertEdge(3, 7, 1);
        graph.insertEdge(4, 7, 1);
        graph.insertEdge(2, 5, 1);
        graph.insertEdge(2, 6, 1);
        graph.insertEdge(5, 6, 1)
        // 打印出
        graph.showGrpah();
    }
}

运行上面的main方法，控制台打印出信息如下

[0, 1, 1, 0, 0, 0, 0, 0]
[1, 0, 0, 1, 1, 0, 0, 0]
[1, 0, 0, 0, 0, 1, 1, 0]
[0, 1, 0, 0, 0, 0, 0, 1]
[0, 1, 0, 0, 0, 0, 0, 1]
[0, 0, 1, 0, 0, 0, 1, 0]
[0, 0, 1, 0, 0, 1, 0, 0]
[0, 0, 0, 1, 1, 0, 0, 0]

通过上面的例子可以得到发现数据为1 的这个顶点的路径是 1->2->4->8->5->3->6->7 ， 或者也有1->2->3->4->5->6->7->8 ， 因为顶点相交是多对多，路径远远不止上面2条。 于是就有了下面的2种算法来求出路径。

在讲步骤之前先讲两个概念，

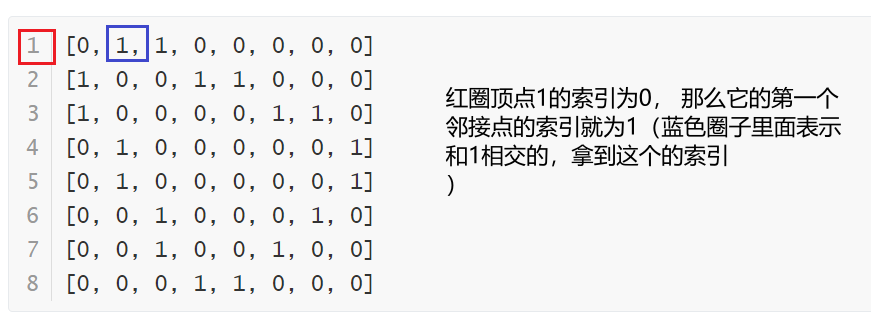
3.2.1 顶点的第一个邻接点

第一个是根据索引拿到该索引的第一个邻接点(索引)， 比如在上面 3.1.2中的数据为1的索引的为0， 那么他的第一个邻接点就为1.

image-20220304132244427

代码如下

        /**
         * 得到该索引的第一个节点
         *
         * @param index
         * @return
         */
        public int getFirtNeighbor(int index) {
            for (int i = 0; i < vertexts.size(); i++) {
                if (edges[index][i] > 0) {
                    return i;
                }
            }
            return -1;
        }

3.2.2 根据前一个邻接点的来获取下一个邻接点的索引

![image-20220304132856641](图算法解析.assets/image-20220304132856641.png代码如下

        /**
         * 根据前一个邻节点来获取下一个邻节点的坐标
         * @param v1 第一个接点的索引
         * @param v2 第一个接点的领节点索引
         * @return
         */
        public int getNextNeighbor(int v1, int v2) {
            for (int i = v2 + 1; i < vertexts.size(); i++) {
                if (edges[v1][i] > 0) {
                    return i;
                }
            }
            return -1;
        }

· One min read

冒泡，交换，选择， 插入

基数排序

shell 快速 归并 堆排序

· 8 min read
jeesk

八皇后问题的程序解答​

在8×8格的国际象棋上摆放8个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法。高斯认为有76种方案。1854年在柏林的象棋杂志上不同的作者发表了40种不同的解，后来有人用图论的方法解出92种结果。如果经过±90度、±180度旋转，和对角线对称变换的摆法看成一类，共有42类。计算机发明后，有多种计算机语言可以编程解决此问题。

由上面的概述可以得出, 任意两个皇后不能处于同一行,同一列, 或者同一斜线. 这条规则是校验八皇后是否合法的规则, 后面的代码将根据这条规则来编写.

1. 回溯法​

​ 首先我们定义一个数组 array = {0 , 4, 7, 5, 2, 6, 1, 3},用单数组表示八皇后的位置,

上面的数组依次表示8皇后在棋盘的位置, array [0] = 0, array [1]=4, array[index] = val ,可以得出每个八皇后的位置在第index+1行,

在(val+1) 列, 入下图所示, 可以看到下面的表格是满足任意两个皇后不能处于同一行,同一列, 或者同一斜线.

1
2
3
4
5
6
7
8

1.1 八皇后的规则校验​

    /**
     * 校验该皇后是否和前面的皇后冲突
     *
     * @param index 第几个皇后(index表示在数组的索引)
     * @return 该皇后的位置是否冲突
     */
    public boolean isJudge(int index) {
        if (index == 0) {
            // 如果是在数组的第一个皇后直接返回不冲突
            return true;
        }
        // 遍历该皇后前面的皇后
        for (int i = 0; i < index; i++) {
            // 1. 判断该皇后是否和前面的皇后在同一列
            if (array[index] == array[i]) {
                // 假如array[0] = 0, array[1]=1, array[2] = 1那么这个就是冲突的
                return false;
            }
            // 2. 判断该皇后是否和其他的皇后在同一条斜线
            // array = {0,1,2,3,4,5,6,7} , 这8个皇后在同一条斜线, 由此可以得到, 他们的差值相等的
            //  第一个皇后在第一行第一列, 第二个皇后在第二行第二列, 第三个皇后在第三行第三列
            //  由此可得第n个皇后和n-个皇后的位置(index)的差值,等于他们所在y轴(val)的差值
            if (Math.abs(array[index] - array[i]) == Math.abs(index - i)) {
                return false;
            }
            // 3. 判断是否在同一行由于我们已经规定好了 array = {0 , 4, 7, 5, 2, 6, 1, 3},
            //    每一个皇后的位置的行在 array[index] =val, 由index 决定,所以肯定不在同一行

        }
        return true;
    }

1.2 放入皇后​

    /**
     * @param index 皇后在数组的位置(index)
     */
    public void putQueue(int index) {
        if (index == max) {
            // 当index = max的时候, 表示皇后已经放了8个, 
            num++;
            printQueue();
            return;
        }

        for (int i = 0; i < max; i++) {
            // 将皇后放入数组, 这里的i代表皇后在棋盘的列
            array[index] = i;
            if (isJudge(index)) {
                // 不冲突, 继续放入皇后到数组
                putQueue(index + 1);
            }
            // 冲突的话, 继续循环放入新的皇后到数组(改变当前皇后的列)
        }
    }

1.3 完整代码如下​


public class Queue8Demo {

    //定义一个max表示共有多少个皇后
    int max = 8;
    //定义数组array, 保存皇后放置位置的结果,比如 arr = {0 , 4, 7, 5, 2, 6, 1, 3}
    int[] array = new int[max];
    // 解法计数器
    static int num = 0;
    
    public static void main(String[] args) {
        long startTime = System.currentTimeMillis();
        Queue8Demo queue8 = new Queue8Demo();
        queue8.putQueue(0);
        System.out.println("耗时:" + (System.currentTimeMillis() - startTime));
    }

    /**
     * 校验该皇后是否和前面的皇后冲突
     *
     * @param index 第几个皇后(index表示在数组的索引)
     * @return 该皇后的位置是否冲突
     */
    public boolean isJudge(int index) {
        if (index == 0) {
            // 如果是在数组的第一个皇后直接返回不冲突
            return true;
        }
        // 遍历该皇后前面的皇后
        for (int i = 0; i < index; i++) {
            // 1. 判断该皇后是否和前面的皇后在同一列
            if (array[index] == array[i]) {
                // 假如array[0] = 0, array[1]=1, array[2] = 1那么这个就是冲突的
                return false;
            }
            // 2. 判断该皇后是否和其他的皇后在同一条斜线
            // array = {0,1,2,3,4,5,6,7} , 这8个皇后在同一条斜线, 由此可以得到, 他们的差值相等的
            //  第一个皇后在第一行第一列, 第二个皇后在第二行第二列, 第三个皇后在第三行第三列
            //  由此可得第n个皇后和n-个皇后的位置(index)的差值,等于他们所在y轴(val)的差值
            if (Math.abs(array[index] - array[i]) == Math.abs(index - i)) {
                return false;
            }
            // 3. 判断是否在同一行由于我们已经规定好了 array = {0 , 4, 7, 5, 2, 6, 1, 3},
            //    每一个皇后的位置的行在 array[index] =val, 由index 决定,所以肯定不在同一行

        }
        return true;
    }


    /**
     * 放入皇后到数组
     * @param index 皇后在数组的位置(index)
     */
    public void putQueue(int index) {
        if (index == max) {
            // 当index = max的时候, 表示皇后已经放了8个,已经得到一种解法
            num++;
            printQueue();
            return;
        }

        for (int i = 0; i < max; i++) {
            // 将皇后放入数组, 这里的i代表皇后在棋盘的列
            array[index] = i;
            if (isJudge(index)) {
                // 不冲突, 继续放入皇后到数组
                putQueue(index + 1);
            }
            // 冲突的话, 继续循环放入新的皇后到数组(改变当前皇后的列)
        }
    }

    public void printQueue() {
        System.out.print("解法" + num + ":");
        for (int i = 0; i < array.length; i++) {
            System.out.print(array[i]);
        }
        System.out.println();
    }
    
}

总结​

  1. 通过递归解决了八皇后的解法, 学习递归的用法

· 5 min read
jeesk

约瑟夫问题的几种算法​

据说著名犹太历史学家Josephus有过以下的故事：在罗马人占领乔塔帕特后，39 个犹太人与Josephus及他的朋友躲到一个洞中，39个犹太人决定宁愿死也不要被敌人抓到，于是决定了一个自杀方式，41个人排成一个圆圈，由第1个人开始报数，每报数到第3人该人就必须自杀，然后再由下一个重新报数，直到所有人都自杀身亡为止。然而Josephus 和他的朋友并不想遵从。首先从一个人开始，越过k-2个人（因为第一个人已经被越过），并杀掉第k个人。接着，再越过k-1个人，并杀掉第k个人。这个过程沿着圆圈一直进行，直到最终只剩下一个人留下，这个人就可以继续活着。问题是，给定了和，一开始要站在什么地方才能避免被处决。Josephus要他的朋友先假装遵从，他将朋友与自己安排在第16个与第31个位置，于是逃过了这场死亡游戏

现在简单的举个例子:

假如一共有8个, 从第一个开始报数, 然后每次报3个人出圈

1,2,3,4,5,6,7,8

  1. 1,2,3,4,5,6,7,8 3号出圈
  2. 1,2,4,5,6,7,8 6号出圈
  3. 1,2,4,5,7,8 1号出圈
  4. 2,4,5,7,8 5号出圈
  5. 2,4,7,8 2号出圈
  6. 4,7,8 8号出圈
  7. 4,7 4号出圈
  8. ​ 7

现在大家应该是明白了, 约瑟夫算法的玩法, 那么下面分享几种不同思路的解法

1. 环形链表解法​

1.1 思路分析​

  1. 首先是拿到环形链表的第一个数据first , 和最后一个数据last
  2. 在报数的时候, 循环报数, 每次first 和last 移动(m-1)次, 然后删除当前节点, 相当于出圈
  3. 当过first= last的时候, 只有最后一个人了

1.2 代码实战​

package com.shanjiancaofu;

public class JosephuQuestion {
    public static void main(String[] args) {
        LinkedCircle linkedCircle = new LinkedCircle();
        // 增加8个人, 计算出圈的人
        linkedCircle.addEle(8);
        linkedCircle.calu(1, 3);
    }

    public static class LinkedCircle {
        
        /**
         * @param startNo  从第几个人开始数
         * @param countNum 报数
         */
        public void calu(int startNo, int countNum) {
            // 找到最后一个数据
            Element lastEle = first;
            while (true) {
                if (lastEle.getNext() == first) {
                    break;
                }
                lastEle = lastEle.getNext();
            }

            // 将lastEle和first 移动(startNo-1), 这里移动的原因是因为实际情况可能不是从第一个人开始报数
            for (int i = 0; i < startNo - 1; i++) {
                lastEle = lastEle.getNext();
                first = first.next;
            }

            // 循环报数
            while (true) {
                if (lastEle == first) {
                    // 只有一个数据
                    break;
                }
                // 执行报数, 移动first数据,找到出圈的人
                for (int i = 0; i < countNum - 1; i++) {
                    lastEle = lastEle.getNext();
                    first = first.next;
                }
                // 得到的first 就是移除圈的人
                System.out.println("移除圈的人NO:" + first.getNo());
                first = first.next;
                lastEle.setNext(first);
            }

        }


        private Element first;

        /**
         * 增加几个数据
         *
         * @param nums 增加的数据个数
         */
        public void addEle(int nums) {
            if (nums <= 0) {
                System.out.println("参数异常");
                return;
            }
            // 链表的最后一个数据
            Element lastElement = null;

            for (int i = 1; i <= nums; i++) {
                Element element = new Element();
                element.setNo(i);
                if (i == 1) {
                    // 第一个数据是first, 并且first的next也是first自己
                    first = element;
                    first.setNext(first);
                    lastElement = first;
                } else {
                    // 其他的数据next是first,
                    element.next = first;
                    // 设置上一个数据的next是最后一个数据
                    lastElement.next = element;
                    // 并且更新lastElelment为最后一个数据
                    lastElement = element;
                }
            }
        }


        /**
         * 数据
         */
        public static class Element {
            // 数据编号
            private int no;
            // 下一个为数据
            private Element next;

            public int getNo() {
                return no;
            }

            public void setNo(int no) {
                this.no = no;
            }

            public Element getNext() {
                return next;
            }

            public void setNext(Element next) {
                this.next = next;
            }
        }
    }

}

1.3 控制台如下​

移除圈的人NO:3
移除圈的人NO:6
移除圈的人NO:1
移除圈的人NO:5
移除圈的人NO:2
移除圈的人NO:8
移除圈的人NO:4